| Additional Evidence regarding Fertility and Mortality Trends in South Africa and Implications for Population Projections Eric O. Udjo Directorate of Analysis Statistics SA Pretoria Summary Introduction The size of a country’s population at a given point in time can be estimated on the basis of information about the initial base population, and the components of population growth (fertility, mortality and migration). Information about fertility and mortality in South Africa is fragmentary, and this has resulted in diverse estimates of the country’s population size at different time periods. The levels and trends of fertility and mortality in South Africa using information from the 1995 October household survey (OHS95) were first estimated by Udjo in 1997. A number of assumptions were made due to lack of data, or deficiencies in the data, or both - especially with regard to mortality. Fertility and mortality questions
were included in the first democratic census conducted in South Africa in October 1996
(Census 96). Analysis of the responses to the appropriate questions could provide
corroborative evidence (or otherwise) for the results derived from the OHS95. It is
against this background that this study has been undertaken. Objectives The objectives of this study are:
Methods The estimations of
fertility and mortality were based on methods developed by Brass that were designed to
detect and adjust for reporting errors typically observed in demographic data from less
developed countries. Using the fertility and mortality estimates, three sets of population
projections were made based on the cohort-component method. The projections did not take
account of net migration due to lack of reliable data in the form required by the method. Results
Conclusion The results from the present
analysis corroborate those obtained in the earlier study by Udjo - that the size of South
Africa’s population is smaller than hitherto estimated – however, additional
studies are needed to confirm this.
Additional Evidence regarding Fertility and Mortality Trends in South Africa and Implications for Population Projections Introduction The levels and trends of fertility and mortality in South Africa using information from the 1995 October household survey (OHS95) were estimated by Udjo (1997). The results indicated that fertility had declined from 4,2 in 1980 through 3,5 in 1985 and 3,3 in 1990, to 3,2 in 1995. Female life expectancy at birth was estimated to have increased from 51,3 years in 1970 to 55,5 years in 1975, 59,4 years in 1980, 62,9 years in 1985 and 64,9 years in 1995. On the basis of these estimates, the population of South Africa was projected from 1970 to 1996, using the 1970 census as a base. Due to lack of the appropriate, data, migration was not taken into account. According to the projections, the population of South Africa was between 37,5 million and 39,2 million in 1996 excluding the effects of migration. A number of assumptions were made in the study due to lack of data, or deficiencies in the data, or both - especially with regard to mortality. The following assumptions are particularly noteworthy:
Fertility and mortality questions
were included in the first democratic census conducted in South Africa in October 1996
(Census 96). Analysis of the responses to the appropriate questions could provide
corroborative evidence (or otherwise) for the results derived from the OHS95. It is
against this background that this study has been undertaken. The objectives of this study are:
The analysis presented in this study is based on the 1996 South African population census. Methods Although analyses of fertility are usually confined to women of reproductive age (i.e. aged 15-49 years) this author has noted the fieldwork advantage of extending the age limit for the fertility (and childhood mortality) questions beyond the conventional reproductive age by setting a lower and an upper limit as was the case during Census 96. Women aged twelve years or older at the time of the census, were asked how many live births they had ever had (i. e. children ever born). In addition, women who were fifty years old or between the ages of 12 and 14 years at the time of the census were asked how many children they had given birth to during the last twelve months (i.e. current births). Although this study uses the conventional reproductive age group, given the age limits set in the census, any tendencies by interviewers to exclude women close to the upper and lower limits of the reproductive age-group in order to reduce the work-load (see Udjo, 1985) would have been reduced. Tabulation of the number of current births showed that some women reported having had up to nine births within the last 12 months before the census. It is not biologically possible for women to have nine single births within one year (see Bongaarts, 1978). Other than multiple births, one should not expect women to have more than two live births within 12 months. Because birth histories are not collected in censuses, it is not possible to identify multiple births among those reported as current births in Census 96, the reported maximum number of live births within the last 12 months used in this analysis is six. This was regarded as sufficiently flexible to allow for multiple births, taking into consideration international practice. For example, the upper limit set by the Demographic and Health Surveys (DHS) in the input/output database in the following countries were as follows. For births within the 12 months, it was four in Botswana and Ghana, and for births within the last five years, it was six in Botswana, Ghana, Zambia, and Zimbabwe. (See the ISSA data dictionaries). As a starting point, it is now common practice in demography to use Brass (1968) P/F ratio method (or its variants) to analyse the number of children ever born (CEB) and births within the last 12 months (current births) reported by women of reproductive age during a survey or census. The method assumes that fertility has been constant in recent years, and errors in the data on current births are not correlated with the age of the mother. In the application of the method, mean parity equivalents, Fis are estimated and compared with reported mean parities Pis. The ratios of P/Fs by age serve as indicators of the consistency and accuracy of the two sets of data. If fertility in a population has not been constant in recent years, it would not be appropriate to estimate the level using the P/F ratio method since the assumption of constant fertility would be violated. However, one could still use the method to analyse the trend in fertility. Although Arriaga (1983) has shown how the P/F ratio method can be used to estimate fertility when fertility has been changing in a population, initial examination of CEB and current births reported during Census 96 was based on Brass method. The estimation of fertility was based on the Relational Gompertz model. The equation for fitting the model to current fertility is: z(x)-e(x) = a + 0.48(b -1)2 + g(x) where z(x) is -log[-log Fx/F(x+5)], where Fx is cumulated age specific fertility rates (ASFR) up to age x, e(x) and g(x) are tabulated standard values (see Booth, 1979); 0.48 is a constant. From average number of CEB (mean parities), z(i) is -log[-log Pi/P(i +1)] , where Pi is the mean parity in the age group i. (See Zaba, 1981, and Brass 1974, 1996 for details). The application of the method to cross sectional fertility data is explained among others, by Brass (1981), Zaba (1981) and Udjo (1991,1995,1996, and forthcoming, 1998). Arriaga’s method was applied to CEB and current births reported during Census 96 and compared with the estimate obtained from the Relational Gompertz model. Arriaga’s method does not require an assumption of constant fertility. The method can be applied when data on children ever born and the age pattern of fertility are available for two or more enumerations. But when the data are available for only one date, it assumes that fertility was constant during the past as in the case of the Brass method. The estimated total fertility
rate (TFR) from Census 96 was compared with the reported age distributions during the
census, using Rele’s method. The method estimates TFR for one or two 5-year periods
prior to the enumeration, using information on the age distribution of women and children,
and life expectancy at birth. The rationale for the method is the observed relationship
between the ratio of children to women and fertility in a population taking into
consideration mortality. See Arriaga (1994) for details. Mortality In addition to CEB, women aged twelve years and above were asked how many of their children were still alive at the time of the census. These two sets of information were tabulated by 5-year age group for women in the reproductive age to derive proportions dead of children ever born by age of women. Life table survival probabilities among children at different ages were estimated from this information using Brass (1971) technique and refinements by Fernandez (1985, 1989). The method converts proportions dead of children ever born by age of mothers, to probabilities of dying between birth and certain exact ages using the following equation: qx = DiKi
, The appropriate set of multipliers for a particular population are determined by the mean age of the fertility schedule, m, and the ratio of mean parity of women aged 15-19 years to that of women aged 20-24 years, p1/p2, or the ratio of mean parity of women aged 20-24 to that of women aged 25-29, p2/p3. In this study, m and p2/p3 were used for selecting the multipliers. Coale and Demeny (See Brass, 1971) have shown that p2/p3 is more satisfactory for estimating q2, q3 and q5. Using several data sets from the World Fertility Surveys (WFS), Fernandez (1985) showed that the proportions dead of children everborn from women aged15-19 and to some extent, from women aged 20-34, give childhood mortality estimates that are higher than the average for the population. The qx values derived from the Brass method were therefore adjusted using Fernandez coefficients. The adjusted qx were converted into a values (level of childhood mortality) in Brass logit system (1971). The time locations of the a values were estimated using Brass (1985) method.
Brass (1971) developed a method (the orphanhood method) for translating the proportions of persons with a surviving parent into probabilities of survival. The relevant question was asked in Census 96 - Is the (person’s) own mother/father still alive? To calculate probabilities of survival from a base age B, to age B+N the following equation is used: lB+N/lB=WN(5PN-5) + 5PN (1-WN) where lB+N/lB
is the probability of surviving from a base age B, to B+N, N is the central age between two
adjacent five-year age groups; The lB+N/lB values
were translated into levels of adult mortality, a in Brass logit system. The time location
of the a values was estimated using Bamgboye (1982), and Brass and Bamgboye (1982) method.
The applications of the methods to orphanhood data are described among others, by Udjo
(1987, 1991, 1995). The construction of life tables from the childhood and orphanhood estimates were based on Brass two-parameter logit system using the African standard life table. The procedures involved are described by Udjo (1991). The two parameters in Brass logit system are a and b . The former defines the level while the latter defines the relationship of childhood and adult mortality in a population. The two parameters of the logit system correspond to the two factors which Ledermamn and Breas (1959) found to be the most important in explaining variation in the mortality schedule among populations. In outlining some general principles in population estimates, Shryock, Siegal and Associates (1976) have noted the following: "more accurate estimates can generally be made for an entire country than for geographic subdivisions of the country. The national population is much more likely to be closed than is that of a subdivision of a country. ------ In general, more direct data, data of better quality and more information on how to adjust these data for deficiencies, are available for the larger areas, particularly for entire countries, than for smaller areas, the size of small populations may fluctuate widely, with the result that accurate estimation is extremely difficult or impossible. ----- It is usually advisable, therefore, to adjust estimates of geographic subareas to agree with an independently estimated area total; eg. Estimates for provinces should be adjusted to the national total". "More accurate estimates can generally be made for the total population of an area than for the demographic characteristics of the population of the area. Fewer data and data of poorer quality are usually available for making estimates of the population of a given area classified by age, color, sex and other characteristics than of the total population of the area. It is usually advisable, therefore, to adjust estimates of such classes to the area total for the characteristics". On the basis of the above principles, estimates of the national population usually precede estimates of its subgeographical and demographic characteristics. Accordingly, the U.S Bureau of Census in its projection of population of states, adjusted the final results of the states projections by race etc to be consistent with the national projections by age sex, and race. (See U.S. Bureau of Census in, U.N., 1993). The general principles outlined
above have been adopted in this study. Only the national population estimates have been
attempted at this stage. The second stage of this study would be to estimate the
demographic parameters of the South African population by province and population group
and their implications for population projections. The subnational estimates that would be
carried out would be adjusted to the national estimates presented in this study. The base population of the projections The base period of the projections of the national population in this study is 1970. Three base population figures by age and sex were used in the projections:
Age and sex distributions of the
CSS adjusted figure were obtained by applying the overall sex ratio and proportionate
age-sex distributions of the unadjusted 1970 census count to the CSS adjusted census
population for 1970. The distributions of the base population figure by age and sex are
shown in appendix 1. The estimates of fertility from the previous study and the fertility estimate obtained from the 1996 census were used as inputs in the projections. It was assumed that the level of fertility indicated in 1996 was the same as in 1995. The mortality inputs were obtained from the 1996 census. An improbably high level of male adult mortality was indicated in the 1996 census, as was also the case in OHS95 (Udjo, 1997). Life expectancy at birth was assumed to be six years higher among males compared to females in the population, for each of the projection periods in this study (five years in the previous study). The justification for choosing a six-year difference in male-female life expectancy at birth was based on the following observations. Recent data from the Population Reference Bureau (see Population Reference Bureau: World 1995 World Population Data Sheet) suggest that in 1995 male-female life expectancies at birth were:
In addition, regression analysis undertaken by the United Nations (1982) on male-female differences in life expectancies at birth and at age 10 for countries in sub-Saharan Africa, Latin America and Far East Asia suggest a difference of 4,7 years for a life expectancy at birth of 60 years. The above observations are also consistent with estimates of male-female differences in mortality provided by Blacker, Hill and Timaeus (1985) for some African countries. In their study, the a and b parameters of the logit system for several African populations in the 1970s – 1980s were estimated. Using these parameter estimates, this author constructed life tables for three countries using Brass African Standard. The male-female differences in life expectancy at birth derived from their parameter estimates were as follows: Malawi (2,1 years), Lesotho (3,9 years); Botswana (5,6 years); Swaziland (8,2 years). With the exception of Botswana, in the other three countries, male-female expectations of life at birth were below 50 years. Within the South African context, it has been suggested that the difference in male-female life expectancy at birth is seven years or more. However, Bradshaw, Dorrington and Sitas (1992) using published life tables and recorded deaths, observed that in 1995 life expectancy at birth in South Africa was about six years higher for females than for males. It is against this background
that the male-female difference in expectation of life at birth of six years was assumed
in this study. Reliable vital registration
systems provide the strongest basis for firmly establishing sex ratios at birth in human
populations. In common with most African countries, vital registration statistics are
incomplete at the national level in South Africa. Blacker in a study (see UNECA, 1968)
made the following observations: "There is a great shortage of reliable data on
the sex ratio at birth in Africa, but there is reason to suppose that it may be somewhat
lower than in most European, Asian and Latin American countries. In the absence of any
trustworthy indications to the contrary, it is suggested that for countries south of the
Sahara ........ sex ratio at birth of 103 should be adopted, while for North African
countries 105 or 106 may be more appropriate. In another study, Udjo (1994) suggested
that the sex ratio at birth in Botswana is perhaps close to 102. There are certain
features of Botswana’s demographic characteristics that are similar to South
Africa’s, the sex ratio at birth in Botswana may not be very different from at least,
the major population group in South Africa. In view of the above, and given that about 24%
of South Africa’s population is non-black, a sex ratio at birth of 103 was assumed in
the projections. Due to lack of appropriate data,
net migration was not taken into account in the projections. Three sets of projections were made which, for convenience are referred to as the low, medium and high variants. The low variant is based on the unadjusted 1970 census population; the medium variant is based on the adjusted 1970 census population (Sadie, 1998) while the high variant is based on CSS adjusted 1970 census population. The fertility and mortality inputs in the projections are the same in the three variants. The projections were based on the
cohort-component method (see Shryock, Siegal and Associates, 1976) using the computer
software, DemProj prepared by the Futures Group (1976). Results Table 1: Brass P/F ratios based on Census 1996 using Hamad’s multipliers
Table 1 shows the application of the P/F ratio method using a refined model by Hamad (1982). The observed mean age of the fertility schedule (31,6), was out of range of the tabulated values for selecting the multipliers. It was therefore necessary to estimate "m" indirectly from Brass’ (1985) table on time location of childhood mortality using the observed ratio of the mean parity of women aged 20-24 years to that of women aged 25-29 years, p2/p3. As can be seen in Table 1, the P/F ratios are greater than 1 and decline as the age of mothers increases. Declining P/F ratios usually indicate underreporting of current births. The reported TFR of 3,0 appears implausibly low. While at face value the declining series of P/F ratios could mean that fertility is currently rising it could also mean any combination, or all the following:
Insight into the nature of the
error was sought by fitting the Relational Gompertz model. The results are shown in Tables
2 and 3 and illustrated in Figure 1. While both the F and P points curve downward at the
older ages, the curve is less pronounced for the P points (Figure 1). This pattern is
suggestive of age exaggeration. Since the curving downward is more pronounced for the F
points, a straight line was fitted to the P points by the group average method, ignoring
the last point, since it was an outlier. Table 2: Fitting the relational Gompertz model to age specific fertility rates from Census 1996
Figure 1: Fitting the relational Gompertz
model 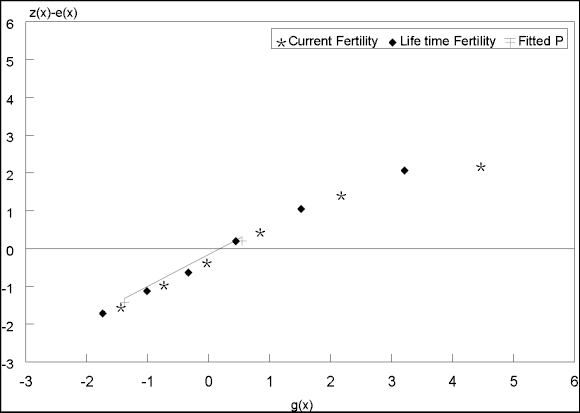
a = 0,111 TFR = 3,3 The Gompertz parameters were
estimated from the fitted line and then applied to the standard values to obtain the TFR
for 1996. The average of the TFRs derived from all the age groups, yielded a TFR of 3,3.
The estimated Gompertz parameters and TFR are shown underneath Table 3. Adjusted age
specific fertility rates (ASFRs) were obtained by applying the parameters to the standard
values of cumulated fertility rates. The results were then applied to the estimated TFR to
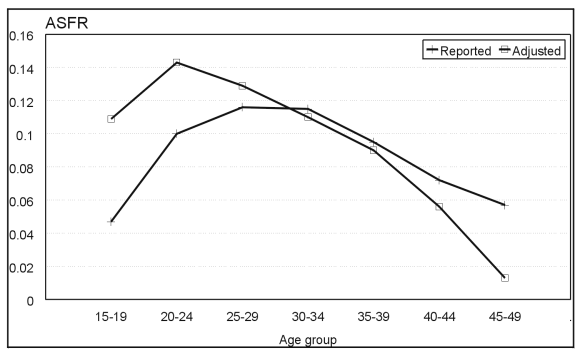
obtain adjusted ASFRs. Figure 2: Reported and adjusted age specific fertility rates from Census 1996
Figure 2 shows the reported and
adjusted ASFRs. The pattern is atypical of what is known about the age pattern of
fertility for human populations. The adjusted ASFRs is closer to the pattern published for
Southern Africa by the United Nations (1997). The selection of the appropriate multipliers for converting the reported proportions dead of children ever born were based on the reported p2/p3, and an indirectly estimated "m" as explained above. The parameters for selecting the appropriate adjustment factors of qx values in Fernandez (1985) were:
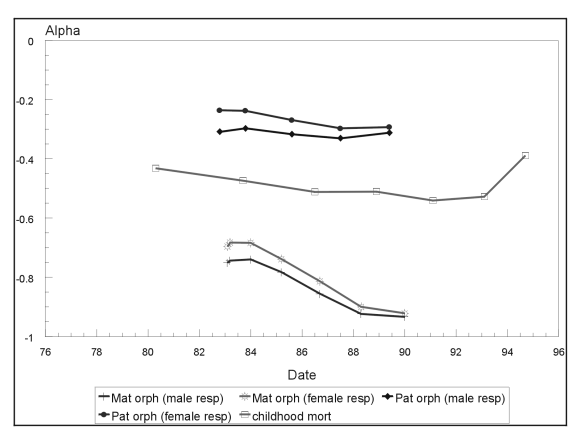
Figure 3 : Trend in mortality from Census 1996
The results are shown in Table 4
and illustrated in Figure 3. There is no obvious indication of underreporting of children
dead from the adjusted qx pattern (Table 3). The a values suggest a moderate
level of childhood mortality. The time trend in a (Figure 3) suggests a modest decline in
childhood mortality between 1980 and 1994 and an increase in recent years. The question
which arises, is whether or not the upward trend in recent years is a true reflection of
child mortality, or is merely an artefact of the data. Note that usually, the qx values
for younger women (on which the a values are based) have been adjusted, yet the trend in
childhood mortality in recent years indicates a worsening situation. Further research on
the trend in childhood mortality in recent years is needed. The observed female mean age of child bearing "M" of 30,7 years, was out of range of Brass tabulated values. The indirectly estimated "m" (as explained above) was therefore used as an estimate of M in selecting the appropriate multipliers for converting the proportions of persons with a surviving mother into probabilities of survival. The analysis was done by sex because male and female responses to the census question regarding surviving parents were different.
Table 5a: Adult female mortality
from reports of mothers alive
The results of maternal orphanhood are shown in Tables 5a and 5b and illustrated in Figure 3. Tables 5a and 5b show that, the proportions of male respondents reporting mother alive is higher than the corresponding proportion of female respondents. This pattern has been observed in the data of other African countries. Blacker (1977) attributes this to differential age misreporting. Accordingly, males have a tendency to exaggerate their ages, and since the proportions with mother alive falls rapidly with increasing age of respondents, any exaggeration of reported ages mean that the proportions with living mothers would be biased upward.M = 28,3
Table 5b: Adult female mortality
from reports of mothers alive
On another note, Blacker (1977) observed that "in Africa, the words ‘father’ and ‘mother’ are often used loosely to denote not only a person’s biological parents, but also foster parents, or older relatives acting, perhaps temporarily, in loco parentis, or simply as terms of respect for members of an older generation. ---- The substitution of foster parents for true parents in the response might clearly lead to serious bias, since the process of adoption may take place because of the mortality one is trying to measure". Within the South African context, Mandela (1994) has noted that "In African culture, ---- we do not make the same distinctions among relations practised by whites. We have no half-brothers or half-sisters. My mother’s sister is my mother; my uncle’s son is my brother; my brother’s child is my son, my daughter (emphasis mine)". The trend in maternal orphanhood from Census 96 is inconsistent with that obtained from the OHS95 data. The estimates from the census show a steeper decline than those obtained from the OHS95 even though the time periods are somewhat similar. In view of the above, the
relationship between female adult mortality and childhood mortality was based on the
childhood mortality estimates and the report of older women aged 30-49 years reporting
mother alive. The level of female adult mortality in this age group is consistent with
that obtained from the OHS95. Usually, there are problems in estimating "M" for males in any population. (See Brass,1975). In accordance with Brass’ proposal, M was estimated by adding a constant to the estimated female M. In the present study, this constant is 2,3 years - the difference between the estimated male and female SMAMs. On the basis of this, the appropriate multipliers were selected and used in converting the proportions of persons with a surviving father into probabilities of survival. The results are shown in Tables 6a and 6b. Similar to maternal orphanhood, the proportions of male respondents reporting father alive is higher than the corresponding proportion of female respondents. Consequently, the level of male adult mortality implied by the proportions of female respondents reporting father alive is higher than the corresponding level implied by the proportion of male respondents.
M = 33,0 Table 6b: Adult male mortality from reports of fathers alive from Census 1996 (female respondents)
M = 33,0 The a values indicate improbably high levels of male adult mortality. Similar levels were observed in OHS95 data. It would appear that for reasons not quite clear, mortality of fathers is overstated in South Africa. When the a values were combined with those from childhood mortality to define the relationship between childhood and male adult mortality, they implied b values that were improbably high and inconsistent with those obtained by combining the childhood and maternal orphanhood a values. The resulting b values from childhood mortality and male adult mortality were also inconsistent with those obtained from several other countries in sub-Saharan Africa. For example, Blacker, Hill and Timaeus (1985) found that, among the seventeen sub-Saharan African countries studied, male b values were greater than 1 in only three countries - Mali, Lesotho, and Ghana. Although the trend in male adult
mortality (Figure 3) is plausible, the levels appear too high and were therefore not used
in further analysis. In view of the weaknesses of the mortality data outlined above, time period two-parameter logit life tables were constructed for quinquennial years from 1970-1990, and for 1996. The observed annual improvement in childhood mortality between 1980 and 1991 was approximately -0.010 in terms of a . Childhood mortality was linearly extrapolated backward to 1970 and forward to 1996 on the basis of this trend. The values derived from the older female respondents (aged 30-49 years) were averaged yielding a value of about –0.688. On the assumption that trend in female adult mortality is similar to the observed trend in childhood mortality, the trend in female adult mortality was extrapolated backward to 1970 and forward to 1996 based on the trend in childhood mortality between 1980 and 1991. On the basis of the a values
derived from these extrapolations (Table 7a), the relationship of childhood mortality and
female adult mortality was defined by constructing hybrid life tables (using the Brass
African Standard) for each of the time periods shown in Table 7a. The two parameters (a
and b ) of the logit life table were then estimated. The procedure is described by Udjo
(1991)and the results are shown in Table 7b. Table 7a: Time period female a values from Census 1996
Table 7b: Estimated parameters of the female logit life table from Census 1996
Table 8: Estimated time period indices of female mortality from Census 1996
Evaluation of the fertility and mortality estimates One needs to be cautious in comparing the fertility and mortality estimates obtained by Udjo (1997) and those presented here (by the same author) with other estimates for the following reasons:
In light of the above, the comparisons in the section which follows should therefore be interpreted with caution. As noted above, Arriaga (1983) has shown how the P/F ratio method can be used to estimate fertility when fertility has been changing in a population. The use of this model on the basis of Census 96 data alone was inappropriate because, in common with the Brass method, it assumes fertility has been constant during the past, when information on CEB and pattern of fertility are available for only one date. To address this limitation, the model was applied using reported CEB and ASFRs from both OHS95 and Census 96 so that two data points were used. Despite this modification, the results were largely meaningless.
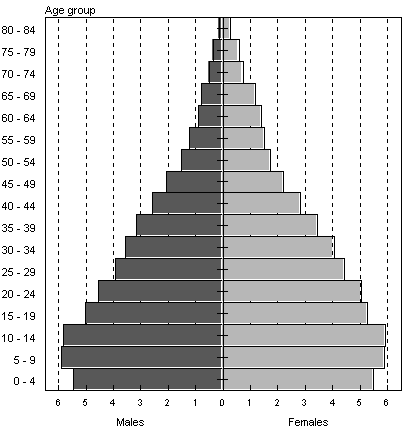
Figure 4: Unadjusted age-sex
distribution from Census 1996
Rele’s technique was used to estimate TFR from the age distribution in Census 96. The TFR was then compared with the estimates derived from the Relational Gompertz model. Note that Rele’s technique is a form of reverse-survival method. As noted by the United Nations (1983), reverse survival techniques "are all heavily dependent upon the accuracy of the reported age distribution of the population being studied. Errors in age-reporting or differential completeness of enumeration affecting certain age groups, especially the younger ones, are certain to bias the estimates obtained. Because these types of deficiencies are all too frequently characteristic of the data sets available, reverse-survival methods are often ineffective in producing reliable fertility estimates". The implied level of TFR using Rele’s technique based on the reported ratio of children aged 0-4 years to women aged 15-49 years during Census 96 is 2,92 which corresponds to a time period 1994. This implied level of fertility appears too low and suggests under reporting of persons aged 0-4 years during the census. On the other hand, the implied TFR from the ratio of children aged 5-9 years to women aged 20-49 years is 3,66 which corresponds to the period 1989. This appears to be an overestimate for the period due to age shifting of some children aged 0-4 years into the 5-9 year age group (See Figure 4). An average of the estimates derived from these two age groups however implies a TFR of 3,3 for the period 1989-1994. This is consistent with the estimate of 3,2 derived from the OHS95 in the previous study (Udjo, 1997). The estimated TFR of 3,3 for 1996 based on Census 96 (derived from the Relational Gompertz Model) is marginally higher than that for 1995 (3,2) based on OHS95. However, TFRs can change from one year to another due to changes in the tempo of fertility. (See Bongaarts and Feeney, 1998). The TFR for 1996 is also consistent with the estimate reported by Sidiropulous et al (1997) who reported a TFR of 3,3 as the current level of fertility in South Africa. It has been suggested that the estimated TFRs by this author for the 1970s are too low compared to those in other studies. See Chimere-Dan (1993) for a review of time period estimates of TFRs in South Africa. Against this background, this author has used the age distributions of the 1970 census as indicative insight of fertility during the period. Using Rele’s technique the reported number of children aged 0-4 years in the 1970 census implies a TFR of 4,85. In addition, the corresponding value based on the adjusted 0-4 age group (Sadie, 1988) was 5,16. Both estimates relate to 1967 and both are consistent with the fertility rate of 4,9 estimated for the year 1970 by this author. With regard to mortality,
Sidiropoulous et al (1997) reported a female life expectancy at birth of 68 years in South
Africa for the period 1991-96, and infant mortality rate (both sexes) of 56,1 per
thousand. While the former is higher than that estimated for 1996 in this study, the
latter is consistent with the estimated female life expectancy at birth for 1996 in this
study (with the assumption of a 10-point difference in male-female infant mortality rate). Implications of the Results for Population Projections Between 1970 and 1990 the TFRs used in the current projections are similar to those obtained previously (Udjo, 1997). These were combined with the TFR derived from census 96. It was assumed that the level of fertility in 1996 (derived from the 1996 census) was the same as that in 1995. Thus the TFRs were 4,9 in 1970, 4,2 in 1985, in 1990 3,5 and 3,3 in 1995 and 1996. The estimated female life expectancies shown in Table 8 and a difference of six years between female and male life expectancy at birth were used as the mortality inputs. The assumptions about sex ratio at birth and net migration were as explained in the beginning of this paper. On the basis of the above, the population of South Africa was projected from 1970 to 1996 using the cohort component method. The results are shown in Table 9. The estimated population of South Africa in October 1996 on the basis of the projections ranges between 38,3 million in the low variant, and 39,9 million in the high variant (excluding the effects of migration). It has been suggested that a sex
ratio at birth of 102 and a seven year difference between male and female life expectancy
at birth are more appropriate for projecting the population of South Africa. However, when
these are used for the medium variant projections, a population size of 38,6 million in
October 1996 is obtained. On the other hand a 5-year difference between male and female
life expectancy at birth and a sex ratio at birth of 102 produced a population size of
38,9 million.
Table 9: Estimated population of South Africa
The above estimates are higher than those in the earlier study by Udjo (1997). The higher estimates in the present study are due to:
The present study however, has
some weaknesses. As in the previous study, it does not take account of net migration due
to lack of the appropriate data. Among other things, the structure of the population may
have changed since 1970 due to net migration. Hence the sex ratios implied in the
projections may not be an accurate reflection of the South African population today. The
sex ratio at birth was held constant throughout the projection period. Although sex ratio
at birth does not change dramatically in a population, there is evidence that it is not
constant either in a population. For instance, Lassus (1995) has shown how the sex ratio
at birth has varied between 1620 and 1799 in Quebec. Lastly, male adult mortality could
not be reliably estimated as was the case in the previous study. Some of these weaknesses
could be overcome as more reliable data become available. Despite these weaknesses, the
results of this study still lead to the same conclusion as that in the previous that the
size of South Africa’s population is smaller than hitherto estimated. However, more
corroborative studies are needed to confirm this. The author wishes to thank senior management of Stats SA for the encouragement and provision of the infrastructure that made this project possible. In addition, the assistance of the following need special acknowledgement: Jean-Marie Hakizimana who extracted the demographic variables from the census database; Samuel Chaba, Andre Delport, Cornelius Mothoa, Judy van der Linde and especially Celna Human and Johan Spies - all from the Information Technology section - for providing excellent support services; Joyce Lestrade-Jefferis for editing and making this paper more intelligible. Sincere thanks are also due to my
family - Eugenia, Oke and Ogaga - who bore the brunt of the many long hours I was at work
during the course of this study. Arriaga E. E. (1994). Population analysis with microcomputers. Bureau of the Census, USAID and UNFPA, pp 204-205. Arriaga E. E. (1983). Estimating fertility from data on children ever born by age of mother. International Research Document, no. 11. U. S. Bureau of the Census, Washington D. C. Blacker J. G. C., Hill A. G., and Timaeus I. (1985). Age patterns of mortality in Africa: an examination of recent evidence. Paper presented at the International Union for the Scientific Study of Population Conference, Florence. Bongaarts J. (1978). A framework for analyzing the proximate determinants of fertility. Population and Development Review, vol. 4, no. 1, pp.105-132. Bongarts J., and Feeney G. (1998). On the quantum and tempo of fertility. Population and Development Review, vol. 24, no. 22, pp271-291. Booth H. (1979). The estimation of fertility from incomplete cohort data by means of the transformed Gompertz model. Ph.D. Thesis, Faculty of Medicine, University of London (London School of Hygiene and Tropical Medicine). Bradshaw D., Dorringtion R. E., and Sitas F. (1992). The level of mortality in South Africa in 1985 - what does it tell us about health? South African Medical Journal, vol. 82, pp. 237-240. Central Statistical Service (1977). Census’96: Preliminary estimates of the size of the population of South Africa. CSS, pp. 17-25. Brass W. (1968). Methods of analysis and estimation. In, Brass, et al, The Demography of Tropical Africa. Princeton University Press, Princeton. Brass W. (1971). Mortality estimates from children ever born and children surviving. In, Methods for estimating fertility and mortality from limited and defective data. The University of North Carolina at Chapel Hill, pp. 50-59. Brass W. (1974). Perspectives in population prediction: illustrated by statistics of England and Wales. Journal of the Royal Statistical Society, series A 137, part 4, pp. 532-583. Brass W. (1981). The use of the relational Gompertz model to estimate fertility. Proceedings of the International Union for the Scientific Study of Population Conference, Manilla, Liege. Brass W. (1985). A simple approximation for the time location of estimates of child mortality from proportions dead by age of mother. In, Advances in methods for estimating fertility and mortality from limited and defective data. Centre for Population Studies, London School of Hygiene and Tropical Medicine, pp. 1-16. Brass W. (1996). Demographic data analysis in less developed countries: 1946-1996. Population Studies, vol 50, no. 3, pp 451-467. Chimere-Dan O. (1993). Racial patterns of fertility decline in South Africa. In, International Population Conference, Montreal. International union for the Scientific Study of Population, Liege, pp. 43-51. Fernandez C. R. E. (1985). The influence of differentials in child mortality by age of mother, birth order and birth spacing on indirect estimation methods. Ph.D thesis, Faculty of Medicine, University of London (London School of Hygiene and Tropical Medicine). Lederman and Breas. (1959) Les dimensions de la mortalite. Population, no. 4. Fernandez C. R. E. (1989). The effects of maternal age, birth order and birth spacing on indirect estimation of child mortality. Proceedings of the International Union for the Scientific Study of Population Conference, New Delhi. Shryock H. S., Siegal J. S. and Associates (1976). The methods and materials of demography. Academic Press, New York, pp. 409-410. Sidiropoulos E., et al. (1997). South Africa Survey 1996/97. South African Institute of Race Relations, Johannesburg, pp. 10-13. Udjo E. O. (1985). Levels and differentials in fertility and mortality among some Kanuri of north-east Nigeria. Ph.D Thesis, Faculty of Medicine, University of London (London School of Hygiene and Tropical Medicine), p. 35. Udjo E. O. (1987). Levels and trends in infant and child mortality among some Kanuri of N. E. Nigeria. Journal of Tropical Paediatrics, vol 33/1, pp. 43-47. Udjo E. O. (1991). Fertility levels among Nigeria’s Kanuri. GENUS, vol, XLVII no.1-2, pp. 163-176. Udjo E. O. (1991). Adult mortality from information on orphanhood and widowhood among Nigeria’s Kanuri. Journal of Biosocial Science, vol. 23, no. 2, pp. 155-165. Udjo E. O. (1995). Fertility and mortality trends and implications for social demands in Botswana. Southern Africa Journal of Demography, vol. 5, no. 1, pp. 1-10. Udjo E. O. (1995). Childhood and adult mortality patterns in Botswana. In, Central Statistical Office: 1991 Population Census Dissemination Seminar, Government Printers, Gaborone, pp. 131-143. Udjo E. O. (1997). Fertility and mortality trends in South Africa: the evidence from the 1995 October household survey, and implications on population projections. Central Statistical Service, Pretoria. Udjo E. O. (forthcoming). Trends in level and tempo of fertility in Botswana. United Nations (1992). Model life tables for developing countries. U.N., New York, p. 30. United Nations (1993). Readings in population research methodology: population models, projections and estimates. United Nations Population Fund, section 17-58 – 17-65. United Nations Economic Commission for Africa. (1968). The report of the seminar on the organisation and conduct of censuses of population and housing, vol. II, part II, Addis Ababa. Zaba B. (1981). Use of the
Relational Gompertz model in analysing fertility data collected in retrospective surveys.
Centre for Population Studies Working paper 8 1-2, London School of Hygiene and Tropical
Medicine. APPENDIX 1: 1970 Population age-sex distributions
** Source: Sadie J. L. (1988). A reconstruction and projection of demographic movement in South Africa. *** Source: Central Statistical Service (1996).
Statistics in Brief. CSS, Pretoria.
APPENDIX 2a: Implied age distributions from the population projections medium variant mid-year estimates
APPENDIX 2b: Implied age distributions from the population projections high variant mid-year estimates
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||